Designing a Function

From time to time you need a function in procedural content generation. A function with certain properties which can be edited easily. A function of your own design.

First of all you need a tool to plot functions or create triangulations (for 2D/3D functions). I took GNU Octave to design the following functions and than ported the code.

Lets start with a small example. Later I will show you a more complex variant I designed for sound synthesis.

A good start is a picture. Draw it and think about what should happen for a wish list of parameters. Lets assume we would like to have a function which starts at 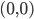and ends at 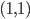. Inside this box we would like to set one point which is on the function. This is a standard interpolation problem but it is a good example and an element of the complex function we will see later.

In next step I always think about other functions which approximate my picture: exp, log, polynomials, sin, cos, ...
Well for our example a line will suffice. The only problem: it must have a break. The easiest thing is to use two lines 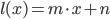and somehow combine them.

The first one goes through 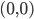and its slope is well defined by 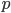. The second one can be defined by a view on the upper corner. Again the slope is a simple quotient 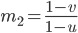which can be put into the line equation 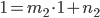and gives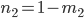

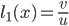
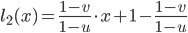
Now we could create a piecewise-defined function or use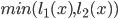. The second variant is valid only for the upper left triangle. It might be useful for another parametrization or function.

My Universal Periodic Function

I searched for a function with a small parameter set which can:

Create high frequent basic tones
Be used for fading of different frequencies
Be used as fade function for the volume

I started with following ideas: A function for a sound must be periodic. I choose 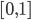as the domain for one period and a co-domain of 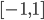because then we have a good control later when using this function. To get something periodic in the interval 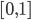we could use fmod or just the fractional part. As long as we define a function in the given interval we do not need to think about periodicity.
Furthermore I would like to be able to mix any standard periodic function (Sinus, Triangle, Square, Sawtooth) by setting parameters. I designed 3 parameters to achieve that:

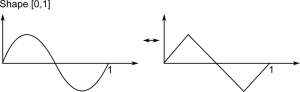Shape: Just interpolate between Sinus and Triangle function. This can be seen as smoothness parameter too. The implementation is as simple as the idea. The triangle function is designed from three lines with slopes 4, -4 and 4 again.

Stretch: 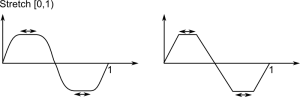Add some space at the vertices of the base functions. This can be used to create a Rectangular function or it is useful for volume and frequency fading too. Just take the first half and you have a function which fades in and out and keeps one level in between.

Shift: Move the vertices left and right (point symmetric). Values near -1 or 1 create a Sawtooth function. Again using only the first half this can be used to control fading.

Moreover Stretch and Shift can be used to design Attack, Sustain and Release of a note. This is not the full ADSR model, but if I can use the same function on many levels it is a good compromise.

Implementation

I started with the implementation of the shape factor. Here I had no better idea than a simple interpolation. The Triangle wave consists of three linear functions: 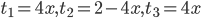. To combine them one could use branches for 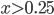and 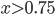, but I expect the usage of min/max to be faster. This time there isn't any parameter which disturbs the ordering of the functions as in the example above.

float upf(float _x, float _shape)
{
	float sinX = sin( _x * PIx2 );
	float triangleX = 4.0f * max(min(_x, 0.5f - _x), _x - 1.0f);

	return lerp(sinX, triangleX, _shape);
}

float upf(float _x, float _shape)

{

float sinX = sin( _x * PIx2 );

float triangleX = 4.0f * max(min(_x, 0.5f - _x), _x - 1.0f);

return lerp(sinX, triangleX, _shape);

}

Afterwards I added the stretch factor. Therefore we must solve the problem: How can we add space at the points 0.25 and 0.75?
Easier is to think: How must x look like that sin(x) will have these plateaus?

So if we have a function as on the picture we are ready. Applying it to x before calling upf(x) adds the plateaus. Moreover we don't need to bother about the shape factor. Its functionality is orthogonal so we can change the parameters independently.

This trick to remap the input is like changing the contrast in a picture. All we need is a monotonous function 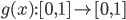and we can change the out coming function while staying inside the given range.

In the implementation I just focused on one single step in , copied that and added 0.5 to the right side.

float stretch(float _x, float _stretch)
{
	// Use only one step function and copy it.
	bool secondHalf = (_x >= 0.5f);
	// The slope if the lines between the constant sections goes from
	// 1 (_stretch = 0) to infinity (rectangular function _stretch = 1).
	if( _stretch == 1 ) return secondHalf ? 0.75f : 0.25f;
	float slope = 1.0f / (1.0f - _stretch);
	_x -= secondHalf ? 0.5f : 0.0f;
	_x *= slope;
	_x = max(min(0.25f, _x), _x - 0.5f * slope * _stretch);
	return secondHalf ? (_x + 0.5f) : _x;
}

float stretch(float _x, float _stretch)

{

// Use only one step function and copy it.

bool secondHalf = (_x >= 0.5f);

// The slope if the lines between the constant sections goes from

// 1 (_stretch = 0) to infinity (rectangular function _stretch = 1).

if( _stretch == 1 ) return secondHalf ? 0.75f : 0.25f;

float slope = 1.0f / (1.0f - _stretch);

_x -= secondHalf ? 0.5f : 0.0f;

_x *= slope;

_x = max(min(0.25f, _x), _x - 0.5f * slope * _stretch);

return secondHalf ? (_x + 0.5f) : _x;

}

Last of all we will add the shift parameter the same way as the stretch parameter. Again a picture can explain that best. Essentially we are using the example from the introduction but we choose the point 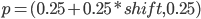. For the right side the same slopes can be used again so three lines (two with the same scope) are created from the one point.

Holding 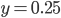is important because we want the shift to move the vertices and no arbitrary points. At the point where the remapping returns 0.25 the vertices are created later which is where we want the change in frequency to happen. I also tested a smoother (exponential) step function but it was less controllable.

float shift(float _x, float _shift)
{
	// Compute the point where the lines should intersect:
	float px = _shift * 0.25f + 0.25f;
	float py = 0.25f;
	// Calculate m*x+n with one of the three lines.
	if( _x < px ) return (py / px) * _x;
	if( _x <= (1.0f-px) ) {
		float m = py / (0.5-px);
		return m * _x + 0.5f - 0.5f * m;
	}
	return (py / px) * _x + 1.0f - (py / px);
}

float shift(float _x, float _shift)

{

// Compute the point where the lines should intersect:

float px = _shift * 0.25f + 0.25f;

float py = 0.25f;

// Calculate m*x+n with one of the three lines.

if( _x < px ) return (py / px) * _x;

if( _x <= (1.0f-px) ) {

float m = py / (0.5-px);

return m * _x + 0.5f - 0.5f * m;

}

return (py / px) * _x + 1.0f - (py / px);

}

This time I consider branching as faster. It is also important to guarantee stability. For parameters -1 and 1 px gets 0. For both cases the branching will end up in the middle part where everything works fine. Otherwise we could get a division by zero.

Summary

Taking all together we have a really customizable function.

float upf(float _x, float _shape, float _stretch, float _shift)
{
	// Make it periodic
	_x -= floor(_x);

	_x = shift(_x, _shift);
	_x = stretch(_x, _stretch);
	return upf(_x, _shape);
}

float upf(float _x, float _shape, float _stretch, float _shift)

{

// Make it periodic

_x -= floor(_x);

_x = shift(_x, _shift);

_x = stretch(_x, _stretch);

return upf(_x, _shape);

}

Except the function shown here I earlier created a light falloff function without a singularity and a determined radius... I could get used to build my own functions. Finally I will give you a list of things I learned:

Use a tool which can plot functions.
Always draw your idea of a function on a paper and than try to find an approximation.
You should know graphs of functions as: sinus, tangents, exp, gauss, ln, polynomials, ...
Linear functions are your friend for parametrization: you will exactly know what they will do.
Many things can be achieved with a polynomial: If you have enough criteria as fixed points and derivatives you can just solve some equations to find the proper factors for a fitting polynomial

Developerblog – Johannes Jendersie

Content Generators & Demos

My Universal Periodic Function

Implementation

Summary

Leave a Reply Cancel reply