The basis for many model generators is an algorithm to turn an implicit surface into a mesh. I implemented different algorithms over the last years and found the famous Marching Cubes painful. There is a bunch of lookup tables and optimizing it creates even more lookup tables. It has to be said that I always try to create vertex and index buffer which means the algorithm must find adjacent triangles fast. However it took me 500 lines code to implement that. This year I discovered another algorithm: Dual Contouring (Marching Edges would fit as name too). I required 200 lines of code to implement it and the performance/quality is good. Dual Contouring creates nicer meshes (more regular triangles) but produces artefacts if objects become too small, which Marching Cubes also do.
The method was invented 2002 and published on the Siggraph: Dual Contouring of Hermite Data. They also compare this method to marching cubes. You might have a look at the pictures to see the differences.
The Idea
In simple words: span a grid, check each edge, if one vertex of the edge is inside and the other outside create a quad perpendicular to that edge, project quad to the isosurface.
Ok the first step is to take a search grid. This grid has some resolution in each direction and determines the detail of the resulting mesh. Whereby cells of that grid must not necessarily be cubes.
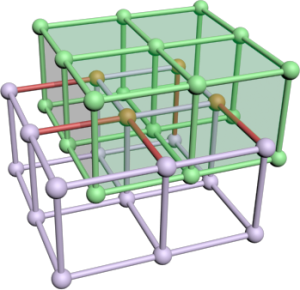Then we just compute the signs for each grid point by sampling of the density/distance function. An edge cuts the isosurface if the two adjacent grid points have a different sign. In that case create 6 new vertices for two triangles spanning a quad. We will resolve the adjacency later. The quad is located at the edge's center and has the same size as the grid in the two perpendicular directions. Assume the green grid to be the edge set of the resulting quads. Rendering that mesh directly creates a voxel-like surface. As the grid image shows the created mesh and the search grid are dual graphs. That is where the name comes from.
Now, only the projection is required. Technically this is done by a gradient descent or conjugated gradient descent algorithm. The gradient might be given by the implicit description of the model or can be estimated by finite differences. Following code snipped computes a variant of the gradient with modified length. If _bLocalLength == false this method returns the normal vector for the vertex at this location. Otherwise the length is scaled by the density value which speeds up the whole gradient descent process by a large factor (~8).
|
1 2 3 4 5 6 7 8 9 10 11 |
static Vec3 Gradient( const ImplicitSurfaces::DensityFunction& _FSurf, const Vec3& _vPosition, bool _bLocalLength ) { Vec3 vGradient; vGradient.x = (_FSurf( Vec3(_vPosition.x+0.05f, _vPosition.y, _vPosition.z) ) - _FSurf( Vec3(_vPosition.x-0.05f, _vPosition.y, _vPosition.z) )); vGradient.y = (_FSurf( Vec3(_vPosition.x, _vPosition.y+0.05f, _vPosition.z) ) - _FSurf( Vec3(_vPosition.x, _vPosition.y-0.05f, _vPosition.z) )); vGradient.z = (_FSurf( Vec3(_vPosition.x, _vPosition.y, _vPosition.z+0.05f) ) - _FSurf( Vec3(_vPosition.x, _vPosition.y, _vPosition.z-0.05f) )); float fLen = 1.0f / len( vGradient ); if( _bLocalLength ) fLen *= _FSurf( _vPosition ); return vGradient * fLen; } |
Doing this on the created triangles directly would mean to compute everything 6 times in average, since at each corner of a "voxel" six triangles meet. Further we would like to have a Indexbuffer for that model to reduce mesh size and increase rendering performance. So there is one intermediate step to find adjacent triangles.
Find Adjacency
Again it just needs a simple idea: Take a hash map, put vertices into, on collision map indices because we have two equal vertices. The main problem is to find an hash function for vertices, which projects very similar vertices to the same value and different vertices to diffferent values. The former is required because there could be little floating-point mistakes. The best thing here is to round the position to three digits and hash the rounded values. Indeed my function looks much more wired because it failed a lot for other meshes (from explicit surfaces). The hashing is still not perfect.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 |
// Compare two vertices if they are very similar. bool operator==(const StdVertex& _v1, const StdVertex& _v2 ) { if( lensq( _v1.vPos-_v2.vPos ) > 0.001f ) return false; if( abs(_v1.vNormal.x-_v2.vNormal.x) > 0.01f ) return false; if( abs(_v1.vNormal.y-_v2.vNormal.y) > 0.01f ) return false; if( abs(_v1.vNormal.z-_v2.vNormal.z) > 0.01f ) return false; return (abs(_v1.u-_v2.u) < 0.01f) && (abs(_v1.v-_v2.v) < 0.01f); } // To make this method fast a "hashmap" is created. Each vertex with // the same position is mapped to the same hash. // This struct is one bucket of the hashmap. struct HashBucket { int aiEntryIndices[8]; ///< Indices of different vertices with the same hash. int iNumEntries; ///< Number of different vertices }; static uint32 IntHash( uint32 a ) { a = (a ^ 61) ^ (a >> 16); a = a + (a << 3); a = a ^ (a >> 4); a = a * 0x27d4eb2d; a = a ^ (a >> 15); return a; } // ********************************************************************* // // Melds all equal vertices and introduces a vertexbuffer. int MeshObj::MeldVertices( int _iNumVertices, StdVertex* _pVertices, uint32* _pIndices ) { uint32 uiHashMapSize = _iNumVertices*2 + 1; int32* pHashMap = (int32*)malloc( sizeof(int32)*uiHashMapSize ); memset( pHashMap, 0xff, sizeof(uint32)*uiHashMapSize ); int iNumRemainingVertices = 0; for( int i=0; i<_iNumVertices; ++i ) { uint32 uiVertexHash = IntHash(uint32(_pVertices[i].vPos.x*1030.9846151)) * IntHash(uint32(_pVertices[i].vPos.y*602.10351258)^0x7ed55d16) * IntHash(uint32(_pVertices[i].vPos.z*2572.98427329)^0xd3a2646c); uint32 uiIndex = uiVertexHash % uiHashMapSize; // Search if there was an equal vertex before this one. Use the // first of them as representative. int j=0; while( (pHashMap[uiIndex] != -1) && !(_pVertices[i] == _pVertices[pHashMap[uiIndex]]) ) uiIndex = (uiIndex+1) % uiHashMapSize; if( pHashMap[uiIndex]==-1 ) { // Nothing found -> this vertex has to be added _pVertices[iNumRemainingVertices] = _pVertices[i]; _pIndices[i] = iNumRemainingVertices; pHashMap[uiIndex] = iNumRemainingVertices; ++iNumRemainingVertices; } else // Reference to the first occurency and forgett the current // vertex. (Do not copy it and do not increase numRemainingVertices. _pIndices[i] = pHashMap[uiIndex]; } free(pHashMap); return iNumRemainingVertices; } |
The
MeldVertices method takes less than a thousandth part of the whole surface extraction process and increases the performance for everything after that step. It could also be used as post process for marching cubes results and other methods.
It should be mentioned that the upper method will fail for more than 8 hash-collisions between different vertices. This small drawback comes from the fact that the implementation is designed for demo (exe files with less than a couple of Kilobytes). You might want to use
std::vector for the bucket or even some tree or
std::unordered_map for the whole hashing.
Now one last image of the beautiful mesh:
You did not use QEFs? I just don't quite get how you take the different normals into account :/
Well, first of all I create the boxy mesh visible in the second picture and meld vertices with the same position. Than I compute the gradient at the position of each vertex via finite differences of my density function. Following the gradient is a search for the root leading to a position on the surface. This position is not necessarily the one with the smallest quadratic error. But this solution is quiet easy and simplicity of code was a major criteria to me. The normal itself is computed as the normalized gradient at the point on the surface at the end.
Hi!
Can you tell me more about "DensityFunction& _FSurf" .
The density function is a function f:R^3 -> R which is similar too a height map in 2D (f:R^2 -> R). Essentially it has areas with values below 0 and other with larger values.
One of the best sources for functions of geometric primitives is: http://www.iquilezles.org/www/articles/distfunctions/distfunctions.htm.
Another interesting article is: http://http.developer.nvidia.com/GPUGems3/gpugems3_ch01.html. In "1.3.3 Making an Interesting Density Function" a function similar to mine is implemented step by step.
Hope that is what you have searched!