Until recently, I usually ignored floating point arithmetic errors in my applications. In graphics you are naturally interested in speed and what does it matter if an object is translated wrongly a thousands part of a pixel? On the other hand: how hard can it be to test if a point lies within a sphere? As formula this is very straight forward: len(center-point) <= radius. Unfortunately this operation involves a sum of squares and the rounding errors indeed lead to wrong classifications. I don't even know how to test if a point is inside a sphere correct without unlimited precision math.

This is a post about different tricks and algorithms to avoid numerical issues. Especially in ray casting and intersection methods I got some artifacts in the past. Many of them occurred to me while writing my math and intersection library Epsilon.

Most of the knowledge here is drawn from the article "What Every Computer Scientist Should Know About Floating-Point Arithmetic" [Go91] and some other articles. I will not go as deep as the linked articles. Instead I will collect what are the most useful algorithms and show some examples when it makes sense to use them. Also, I won't go into details of why there is a numerical issue - for that I recommend to read [Go91].
In the graphs below I computed the relative error of the respective expressions. This is calculated as the result minus the true result divided by the true result, i.e. abs((x-ref)/ref). Thereby, the true result is computed using the most correct expression in double precision.

Rounding

Rounding is the root of all evil. Floats have the nice property that they always have (more or less) the same relative precision. That means, it doesn't matter if a number is small or huge, as long as it is not too small (underflow) or too large (overflow). Still, the number of digits is limited. Lets assume we have 3 digits precision in decimal system, than adding 100e1 and 1 gives 100e1. So the 1 had no effect at all, since the true result 1001 was rounded to three digits. In most cases the rounding during addition is not fatal, because the error is relatively small (all 3 stored digits are correct). Addition and subtraction may only have an error in the last digit, i.e. they will not be far away from the true result. If rounding to the closer number the error is at most 0.5 ulp (units is the last place).

The point where rounding makes things bad is if errors accumulate. In the worst case catastrophic cancellation can happen, where a subtraction of similar numbers reveals a previous error. An example from [Go91]: Again we have decimal numbers with 3 digits: a=1.22, c=2.28, b=3.34  and want to compute b*b-4*a*c. The exact result is 0.0292. In limited precision it is b*b=11.2 (0.5 ulp), 4*a*c=11.1 (0.5 ulp) and finally 0.1 (70 ulp !).

1-x² and x²-y²

Lets start with the smallest term.  1-x*x is very useful in trigonometric expressions, since sin^2 + cos^2 = 1. For example: this can be used for the compression of normal vectors in polar coordinates. So, what is the problem of this expression?
It is catastrophic cancellation, because x is squared and then subtracted, which is the most basic example where this kind of error occurs.
It is possible to write the expression using the third binomial formula (1-x)*(1+x), which is more robust. This form has a bigger error in general, but as the graph shows, its error does not increase if both numbers are very similar and is very small otherwise. However, a maximal error of 0.012% in the first form is not that dramatic for most applications.
Note, that the same trick applies to x*x-y*y  which can be reformulated to (x-y)*(x+y)

Quadratic Equation

There are many algorithms which require the roots of a quadratic polynomial, e.g. a ray-sphere intersection. The basic expression we want to solve is ax² + bx + c = 0 for which the known solution is

If the term below the root gets wrong (like in the example above) this is not that bad, because if that happens the result is small compared to b. Now, the problem occurs again if b and the square root are similar and get subtracted. However, this is only the case for one of the two results, because the other one adds the root term. The graph shows that if b is 1000 times larger than a and c the error becomes already larger than 10% (for 32bit floats). For a factor over 6000, rounding toggles between 100% and some smaller error for odd and even numbers.
Again, it is possible to use the third binomial formula and multiply the term with the denominator using the inverted sign [X05]:

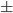Note, that the changed and we get the subtraction for the two results reversed. A stable implementation needs to check which of the two formulas is better for which x and than use one of the two different terms.

ln(1+x) and exp(1+x,n)

For small |x|, 1+x discards many digits, so both expressions will be inaccurate. The later can be useful in numerical integrations (e.g. simulation of movement), when there is a grow or decrease over time. It can be expressed using the first one: exp(1+x,n) = exp(n*ln(1+x)) which leaves us with the problem of ln(1+x) to be inaccurate. Well, if you look at the graph it is not thaaat important. x must be really close to zero, before something bad happens.

The following code snipped solves this issue. Effectively, the function is multiplied with x/x, where the denominator is replaced by (1+x)-1, which is an estimation of the error made by the summation. [HP82]

You can find a numerical stable log1p method in the math.h (at least in my cpp standard library). Surprisingly, it is slower by a factor of 7 and calls modf, acosf, fdtest and log internally. Seems to be some series expansion inside.

Sum and Variance of Many Numbers

Especially path tracing and other Monte Carlo light transport simulations rely on the law of large numbers. I.e. they converge to the correct result for sufficient many samples. Well, they should, but due to floating point they never will.

First, I experimented with plausible series of 10,000 and 100,000 samples of uniform and exponential distributions. All had shown a systematic underestimation with up to 0.001% error. This is only a problem, if many larger numbers with small variance are added (e.g. for being a uniform sample) which I did not test, because this is not really likely for rendering applications. Still, I will add a few solutions for completeness. See [Wiki1] and [He05] for more alternatives. The first well known solution is the Kahan summation. It tracks the lost digits in a second register to achieve a constant error bound (trivial summation has an error in the number of samples). However, adding doubles naively is already more precise than Kahan summation with two floats, so it makes only sense if we want to have even more precision than double [Wiki1] or cannot use double (e.g. on GPU).

Another option is to recursively compute partial sums. This is quite nice, because computing prefix sums (e.g. for summed area tables) with a parallel algorithm is already more accurate than a linear algorithm.

Beyond the sum of samples we could also be interested in there variance. This time errors can get worse, because if the mean 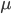is close to the (with a small variance) we subtract two similar numbers.

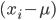Another problem with the naive formulation is, that we need to keep all samples to compute once we know 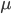. Both problems are solved by Welford's method explained on [Co08]. I like it, because we don't need to store more than three values which we do anyway (mean, variance and number of samples).

Compared to the often used sum of squares method, which stores x, x*x and n, Welford's algorithm performs much better. In the experiment I used n samples uniformly distributed in [0.5, 1.5] which should be comparable stable (see summation above).
Unfortunately, for more than ~45000 samples the variance in the naive sum of squares method gets negative. Even in the absolute value the error gets larger than 1000% (logarithmic scale!). Besides that catastrophe, all other values have acceptable errors in the 5th to 7th decimal place.

Final Thoughts

I tested a set of recipes for numerical stable computations to see which of them are really necessary in the context of rendering and simulation. Before, I encountered problems in a ray tracing application using ellipsoids leading to geometry misses in my bounding volume hierarchy. So, of course I think using the more stable solution of the quadratic polynomial is a good idea.
Using the third binomial formula is not really necessary, but since it barely changes instruction count/performance it can be used everywhere without thinking.
In the cases of logarithmic functions and summing numbers, errors happen in extremal cases mainly. As long as we do not run into these, which is unlikely in rendering, nothing bad happens with the naive approaches.
However, when using the sums of numbers in some subtraction, as for the computation of variance, I strongly recommend to use a better method. Especially, for unbiased Monte Carlo integration simply adding floats is not enough.

[Co08] Accurately Computing Running Variance, John D. Cook, 2008
http://www.johndcook.com/blog/standard_deviation/
[Co14] Avoiding Overflow, Underflow, and Loss of Precision, John D. Cook, 2014
http://www.codeproject.com/Articles/25294/Avoiding-Overflow-Underflow-and-Loss-of-Precision
[Go91] What Every Computer Scientist Should Know About Floating-Point Arithmetic, David Goldberg, 1991
http://docs.oracle.com/cd/E19957-01/806-3568/ncg_goldberg.html
[HP82] HP-15C Advanced Functions Handbook, Hewlett-Packard Company, 1982
[He05] Binary floating point summation accurate to full precision (Python recipe), Raymond Hettinger, 2005
http://code.activestate.com/recipes/393090/
[Wiki1] https://en.wikipedia.org/wiki/Kahan_summation_algorithm
[X05] 2005, http://people.csail.mit.edu/bkph/articles/Quadratics.pdf

In a shader we can type vec3 v0 = v1.xxy * 2 and any other combination of x, y, z and w depending on the length of the vector. The resulting vector must not have the same same size (in the example v1 could be a vec2) because components can be copied through. This is called swizzling and is really comfortable.
Vectors are everywhere in game projects not only in the shaders. How can we get the same behavior in C++? Can we get it without losing performance? I wanted to understand if and how this can be done. There are two solutions available: The glm library from G-Truc and the CxxSwizzle library. Anyway, I did not test the two libraries for their performance but if you wanna have swizzling you might take one of them instead of the header file I had written. The advantage is that they have implemented more functions so far. But, I did not found explanations about how to solve the problem so I will try to fill that gap.

Before we can start here are the problems to face:

• (1) Access the elements in arbitrary order and count: v0.xxy + v1.xzy
• (2) Write to a swizzled vector v1.yxwz = v0;  where doubled elements are explicit forbidden
• (3) No Memory overhead: a vec3 should have the size of 3 times its base type
• (4) No Computational overhead: a solution with multiple lines containing equivalent scalar operations should not be faster

First there are two different possibilities to a achieve the syntax v1.yxwz = v0; without brackets: macros and unions. You could also have a nested type but then the expression would not return any address and it is impossible to calculate things on the data of v without its address. In case of macros you can hide functions like yxwz() which do something you want. The problems with functions is that they get complicated on the left-hand-side where we want them to return references to swizzlings. The example (2) should fill the vector v1 in a swizzled order and not compute things on some copy of v1. You might be able to solve that with template meta programming or explicit proxy objects. These are objects of another type containing a reference to the original type. Operators on them will always access the original elements in some type-dependent way. However Returning proxies might be to complicated for a compiler to be optimized away. Further I do not like to have macros like x to pollute all my namespaces!

The union Solution

In a union all members work on the same space. If each member has a different type and if there are operators for each we can do everything we want.

The types must be trivially copyable, otherwise it would not be possible to put them into a union. It is possible but not feasible to write so many types, so we want the compiler to make this job: using templates.

The Swizzle-Proxy Template

The above class shows the basic idea of how to implement the operators for swizzling with exactly two elements: xx, xy, wx, ... . The template arguments A and B can be any index of elements in an underling real vector. For the swizzle wx  A  is 3 and  B  is 0 accessing two elements of a vec4.

Notice: the class itself does not have own members! Instantiating it would cause lots of access violations. Together with the union above the this  pointer becomes a pointer to m_data . That is why we can cast it so ugly without fear.
Unfortunately when compiling the compiler must create a new operator for each combination of swizzle types. This increases compile times heavily which cannot be avoided.

So far we can use the class the following way:

The second line would also compile but behave wired. It would add v2.z and v2.x to v1.x successively. To avoid that we can cause the compiler to fail by the following trick:

Depending on how the indices are chosen the return type is either SwizzleProxy2 as before or struct OperationNotAvailable which is nowhere defined. In the second case the compiler cannot create the function and will give you an error message which will contain "OperationNotAvailable" at some point.

To implement all the different operators for all SwizzleProxyX class I tried to create a template based collection of common operator implementations. The problem was that the compiler failed to optimize everything so we need to do that ourself for each of the (four) proxy templates. So the old CommonVectorOperator class currently contains the array access operator [] only. To still reduce the work a little bit I used macros for code generation. The macro is undefined at the end of the operator section such that from outside there are no unnecessary symbols. Just have a look into the code of the complete SwizzleProxy2 class.

Remark: The scalar-vector operators are implemented as friend . This is a trick in C++ to avoid having such functions in the global namespace. The compiler can still find the function by ADL (argument dependent lookup). For each different template argument setup of the proxy class there is exactly one such operator.

You might have noticed that the template takes a VectorType argument. This is required in the implementation of the non-assigning operators as a simple +. These must return a new copy which is only possible of the real vector type is known.

The Final Vector Class

If the final class would not inherit from the proxy class operations on normal vectors would not succeed. Instead it would be necessary to write additional operators which take vector-swizzle, vecot-vector and swizzle-vector arguments but fortunately inheritance is much easier.

Then the union is filled with all access patterns up to vec4. As you can see these are 30 for a vec2. For a vec4 itself this number grows to 340 because there are four instead of two indices for each element.

Before the last constructor we would not be able to use all the nice swizzling stuff fluently. Calling move(position.zyx) would fail because .zyx is not a vector (assuming move would like to have a vector). The implicit cast generated through this constructor is rounding off the whole implementation.

Full Header: swizzle.7z
Currently the implementation lacks functions like normalization... They might follow later.