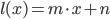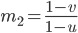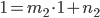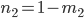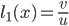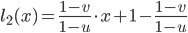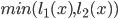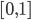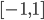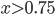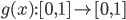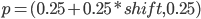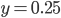Category Archives: Generators

Creation of models and textures through pure code

Hex-Grid Dungeon Generation I

1 Reply

This is the first new post for a series of dungeon generator experiences. As you might expect I have a new game project (since February this year) which is based on a hex-gird. The game mechanic will be something between Hack-n-Slay and Pokémon, but more to that on a dedicated project page later.

First, there is an extremely valuable source for many algorithms appearing on a hex grid: http://www.redblobgames.com/grids/hexagons/ [1]. This side is one of the best web pages I have seen so far. It has very helpful explanations for all hex-grid problems and shows interactive examples for each of them. Moreover, if you change an option in one example, all others adapt to this same option. If you don't understand a detail in this post related to the hex-grid, just have a look on the mentioned side.

Generating Caves on Hex-Grids (Cellular Automaton)

There are many types of dungeons and generators, especially on quad-grids. You can have special maze generators, room based dungeons and caves. This post shows how to generate caves on the hex-grid.

Cellular automata seem to be the most common approach for generating caves. One source I found inspirational is this article [2]. However, I was not able to find sources on good hex-grid cave generator rules quickly, so I started experimenting and here are my results.

The basic idea is to start with a random initialization (floor/wall) and apply some iterations of a cellular automaton. This automaton will check the neighborhood of a cell and decide which type the cell gets in the next turn, based on the number of certain elements in the vicinity. Let 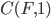being the count of Floor (or Wall) tiles around a cell within a range of 1 excluding the tile itself. This count can be a number in 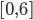. Then, the following rules produced good cave maps:

One important thing is when and how the new type is set. Usually, an automaton would change all states at once, after the types of all cells are determined. Directly changing the cell type will also change the neighborhood of the next cell, which can lead to a fast collapse into a single type only. Luckily the above rule handles direct changes very well. So, yes I am changing types immediately...

Here are two examples with different initialization conditions (60% and 65%), using the same seed. Each row shows the initialization and two iterations.

cave_init60 cave_60_it1 cave_60_it2
cave_init65 cave_65_it1 cave_65_it2

The base shape is determined by the simple fact that I loop over my memory in a rectangle fashion during initialization. It could easily be changed, but I see no need for it. Using the 65% initialization I did not see any caves with large disconnected components on several seeds. If a dungeon is too small it can thus be regenerated with a high success probability. However, even through there are only a few small disconnected components we want to remove them before proceeding with populating the dungeon. It would be a disaster if the boss is in another component and the only way out of a dungeon is killing that boss... Extracting a single component is simply by using a flood-fill.

To make sure we know a good start point, we can modify the initialization. For example, I set all seven tiles around position (0,0) to floor. This gives an area of high floor density which will lead to even more floor tiles in the automaton iteration. It is more likely that the region grows than that it shrinks.

Fractal Noise as Generator

While the above rule is relatively stable, there are no real options to tweak the scale, ... Instead of trying to resample the map as done by [2] to get larger caves I switched to another idea: Generating a fractal noise (Value Noise or Perlin Noise) and using a threshold to determine occupied tiles. Assuming the fractal noise is in [0,1] a threshold of 0.5 should give roughly 50% occupancy. There are several degrees of freedom:

  • The threshold: steers how much of the map is occupied (sparsity)
  • The number of octaves: large scale vs. small scale structures
  • The turbulence function (adding octaves, multiplying, ridged (abs), ...): different shapes

As noise function I used a Perlin Noise with ridged turbulence function. Unfortunately, any noise results in very straight boundaries at the edge of the generation area. Therefore, I gradually increase the threshold to the outer boundary (quadratic over radius of 10 tiles) up to 1.

Of course, there is now guarantee for connected components, but this is the same as for the cellular automaton. I decided to fix this problem with a general approach described in the next section. But, first here some examples of the generator output.  The images have increasing threshold levels which reduces the number of non-empty tiles and increases the chance for non-connected components. The green connections are created by the algorithm below.

cave_perlin_1 cave_perlin_4 cave_perlin_6 cave_perlin_7

Reconnecting Components

Rather than recreating dungeons until they have the right size by accident it is better to somehow increase connectivity. Starting with some known (e.g. (0,0) start position) or a random floor tile one can mark all connected tiles with a flood fill. Then, another unmarked tile can be searched and connected with a randomized work between the start region and the obviously disconnected region. I use an A* way search where empty tiles have a random high cost in [5,20] (fixed for the time of search) and floor tiles have a low constant cost [0.01]. This leads to a non-straight connection between probably close points of the two sets. After connecting the two regions the new part can be marked the same way as the start region (it now belongs to it). When using a simple scan-line as search, all disconnected components will be connected finally.

[1] http://www.redblobgames.com/grids/hexagons/
[2] http://www.roguebasin.com/index.php?title=Cellular_Automata_Method_for_Generating_Random_Cave-Like_Levels

Designing a Function

Leave a reply

From time to time you need a function in procedural content generation. A function with certain properties which can be edited easily. A function of your own design.

First of all you need a tool to plot functions or create triangulations (for 2D/3D functions). I took GNU Octave to design the following functions and than ported the code.

Lets start with a small example. Later I will show you a more complex variant I designed for sound synthesis.Func_Example1

A good start is a picture. Draw it and think about what should happen for a wish list of parameters. Lets assume we would like to have a function which starts at and ends at . Inside this box we would like to set one point which is on the function. This is a standard interpolation problem but it is a good example and an element of the complex function we will see later.

In next step I always think about other functions which approximate my picture: exp, log, polynomials, sin, cos, ...
Well for our example a line will suffice. The only problem: it must have a break. The easiest thing is to use two lines and somehow combine them.

The first one goes through and its slope is well defined by . The second one can be defined by a view on the upper corner. Again the slope is a simple quotient which can be put into the line equation and gives


Now we could create a piecewise-defined function or use. The second variant is valid only for the upper left triangle. It might be useful for another parametrization or function.

My Universal Periodic Function

I searched for a function with a small parameter set which can:

  • Create high frequent basic tones
  • Be used for fading of different frequencies
  • Be used as fade function for the volume

I started with following ideas: A function for a sound must be periodic. I choose as the domain for one period and a co-domain of because then we have a good control later when using this function. To get something periodic in the interval we could use fmod or just the fractional part. As long as we define a function in the given interval we do not need to think about periodicity.
Furthermore I would like to be able to mix any standard periodic function (Sinus, Triangle, Square, Sawtooth) by setting parameters. I designed 3 parameters to achieve that:

Func_ShapeShape: Just interpolate between Sinus and Triangle function. This can be seen as smoothness parameter too. The implementation is as simple as the idea. The triangle function is designed from three lines with slopes 4, -4 and 4 again.

 

Stretch: Func_StretchAdd some space at the vertices of the base functions. This can be used to create a Rectangular function or it is useful for volume and frequency fading too. Just take the first half and you have a function which fades in and out and keeps one level in between.

 

Shift: Func_ShiftMove the vertices left and right (point symmetric). Values near -1 or 1 create a Sawtooth function. Again using only the first half this can be used to control fading.

Moreover Stretch and Shift can be used to design Attack, Sustain and Release of a note. This is not the full ADSR model, but if I can use the same function on many levels it is a good compromise.

Implementation

I started with the implementation of the shape factor. Here I had no better idea than a simple interpolation. The Triangle wave consists of three linear functions: . To combine them one could use branches for and , but I expect the usage of min/max to be faster. This time there isn't any parameter which disturbs the ordering of the functions as in the example above.

Afterwards I added the stretch factor. Therefore we must solve the problem: How can we add space at the points 0.25 and 0.75?
Easier is to think: How must x look like that sin(x) will have these plateaus?

Func_Stretch2So if we have a function as on the picture we are ready. Applying it to x before calling upf(x) adds the plateaus. Moreover we don't need to bother about the shape factor. Its functionality is orthogonal so we can change the parameters independently.

This trick to remap the input is like changing the contrast in a picture. All we need is a monotonous function and we can change the out coming function while staying inside the given range.

In the implementation I just focused on one single step in , copied that and added 0.5 to the right side.

Func_Shift2Last of all we will add the shift parameter the same way as the stretch parameter. Again a picture can explain that best. Essentially we are using the example from the introduction but we choose the point . For the right side the same slopes can be used again so three lines (two with the same scope) are created from the one point.

Holding is important because we want the shift to move the vertices and no arbitrary points. At the point where the remapping returns 0.25 the vertices are created later which is where we want the change in frequency to happen. I also tested a smoother (exponential) step function but it was less controllable.

This time I consider branching as faster. It is also important to guarantee stability. For parameters -1 and 1 px gets 0. For both cases the branching will end up in the middle part where everything works fine. Otherwise we could get a division by zero.

Summary

Taking all together we have a really customizable function.

 

Except the function shown here I earlier created a light falloff function without a singularity and a determined radius... I could get used to build my own functions. Finally I will give you a list of things I learned:

  • Use a tool which can plot functions.
  • Always draw your idea of a function on a paper and than try to find an approximation.
  • You should know graphs of functions as: sinus, tangents, exp, gauss, ln, polynomials, ...
  • Linear functions are your friend for parametrization: you will exactly know what they will do.
  • Many things can be achieved with a polynomial: If you have enough criteria as fixed points and derivatives you can just solve some equations to find the proper factors for a fitting polynomial

Dual Contouring

4 Replies

The basis for many model generators is an algorithm to turn an implicit surface into a mesh. I implemented different algorithms over the last years and found the famous Marching Cubes painful. There is a bunch of lookup tables and optimizing it creates even more lookup tables. It has to be said that I always try to create vertex and index buffer which means the algorithm must find adjacent triangles fast. However it took me 500 lines code to implement that. This year I discovered another algorithm: Dual Contouring (Marching Edges would fit as name too). I required 200 lines of code to implement it and the performance/quality is good. Dual Contouring creates nicer meshes (more regular triangles) but produces artefacts if objects become too small, which Marching Cubes also do.

The method was invented 2002 and published on the Siggraph: Dual Contouring of Hermite Data. They also compare this method to marching cubes. You might have a look at the pictures to see the differences.

The Idea

In simple words: span a grid, check each edge, if one vertex of the edge is inside and the other outside create a quad perpendicular to that edge, project quad to the isosurface.

Ok the first step is to take a search grid. This grid has some resolution in each direction and determines the detail of the resulting mesh. Whereby cells of that grid must not necessarily be cubes.

DualGridThen we just compute the signs for each grid point by sampling of the density/distance function. An edge cuts the isosurface if the two adjacent grid points have a different sign. In that case create 6 new vertices for two triangles spanning a quad. We will resolve the adjacency later. The quad is located at the edge's center and has the same size as the grid in the two perpendicular directions. Assume the green grid to be the edge set of the resulting quads. Rendering that mesh directly creates a voxel-like surface. As the grid image shows the created mesh and the search grid are dual graphs. That is where the name comes from.

DualCountourVoxels

Now, only the projection is required. Technically this is done by a gradient descent or conjugated gradient descent algorithm. The gradient might be given by the implicit description of the model or can be estimated by finite differences. Following code snipped computes a variant of the gradient with modified length. If  _bLocalLength == false  this method returns the normal vector for the vertex at this location. Otherwise the length is scaled by the density value which speeds up the whole gradient descent process by a large factor (~8).

Doing this on the created triangles directly would mean to compute everything 6 times in average, since at each corner of a "voxel" six triangles meet. Further we would like to have a Indexbuffer for that model to reduce mesh size and increase rendering performance. So there is one intermediate step to find adjacent triangles.

Find Adjacency

Again it just needs a simple idea: Take a hash map, put vertices into, on collision map indices because we have two equal vertices. The main problem is to find an hash function for vertices, which projects very similar vertices to the same value and different vertices to diffferent values. The former is required because there could be little floating-point mistakes. The best thing here is to round the position to three digits and hash the rounded values. Indeed my function looks much more wired because it failed a lot for other meshes (from explicit surfaces). The hashing is still not perfect.

The  MeldVertices  method takes less than a thousandth part of the whole surface extraction process and increases the performance for everything after that step. It could also be used as post process for marching cubes results and other methods.
It should be mentioned that the upper method will fail for more than 8 hash-collisions between different vertices. This small drawback comes from the fact that the implementation is designed for demo (exe files with less than a couple of Kilobytes). You might want to use  std::vector  for the bucket or even some tree or  std::unordered_map  for the whole hashing.

Now one last image of the beautiful mesh:

DualCountourProjected