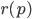The basis for all collision detections is analytical geometry. Math can answer the question where two primitives intersect or give the distance between two objects. This post will only cover such basic functions. So it is a collection of primitive - primitive relation functions. There are two functions given. The first only returns collision or not. The second variant returns a resolvement vector. This is a translation vector which have to be applied to object 1 to move the two objects out of each other.
3D
| Object | Properties |
|---|---|
| Sphere | center  , radius , radius  |
| Line | start and end  , implicit direction , implicit direction  |
| Triangle | The 3 vertices in counter clock wise order 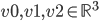 , implicit normal , implicit normal |
Sphere - Sphere

For resolvement just take the connection between the midpoints and the intersection length.

|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
bool SphereSphereCollision( const Sphere& _S1, const Sphere& _S2 ) { float fLen = lensq( _S1.vCenter - _S2.vCenter ); float fr = _S1.fRadius + _S2.fRadius; return fLen <= fr*fr; } bool SphereSphereCollision( const Sphere& _S1, const Sphere& _S2, Vec3& _vResolve ) { _vResolve = _S1.vCenter - _S2.vCenter; float fLen = len( _vResolve ); if( fLen > _S1.fRadius + _S2.fRadius ) return false; fLen = (fLen - (_S1.fRadius + _S2.fRadius)) / fLen; _vResolve *= fLen; return true; } |
Sphere - Line


The resolvement vector is the connection between sphere center and the nearest point on the line.

|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
Vec3 ClosestPointOnLine( const Vec3& _vPoint, const Vec3& _vLineS, const Vec3& _vLineE ) { Vec3 d(_vLineE - _vLineS); Vec3 w(_vPoint - _vLineS); float fR = (dot(w, d) / lensq(d)); // Nearest point to _vPoint is _vLineS if(fR <= 0.0f) return _vLineS; // Nearest point is on the line else if(fR < 1.0f) return _vLineS + d * fR; // Nearest point to _vPoint is _vLineE else return _vLineE; } bool SphereLineCollision( const Sphere& _S, const Line& _L ) { return lensq(_S.vCenter - ClosestPointOnLine( _S.vCenter, _L.vStart, _L.vEnd )) <= _S.fRadius*_S.fRadius; } bool SphereLineCollision( const Sphere& _S, const Line& _L, Vec3& _vResolve ) { _vResolve = _S.vCenter - ClosestPointOnLine( _S.vCenter, _L.vStart, _L.vEnd ); return lensq(_vResolve) <= _S.fRadius*_S.fRadius; } |
Sphere - Triangle
The usual way to do this is to project the sphere center to the triangle's plane. Afterwards the barycentric coordinates of the point would be calculated to test if it is inside. If not we still have to test whether the circle from the plane-sphere cut intersects with a triangle or not. Therefore it is sufficient to test the 3 line-sphere cuts because the center is definitely outside. I changed the middle part to hopefully increase the speed. Instead of calculating the barycentric coordinates I compute the closest points on all three sides which I would need in the last step non the less. Then the following condition must be true if the point is inside: the opposite vertex to a side (and therefore a point on that side) must lie on two different "sides" of the projected center. So the dot product of the vectors from the center to a closest point on a triangle-side and to the related triangle-vertex has to be at least 0.
There was one problem when using a full triangle collision in the game Pathfinder. Imagine a box made of triangles. Then the sphere is placed on top near to an edge. The simulation will first push the sphere down. Afterwards the collision detection would report two triangles. The one on the top and one of a side where the sphere collides with a back face. This has the effect that the sphere is pushed away from the edge to the box center on the upper side. To avoid that I use the condition if( fDist < 0.0f || fDist > _S.fRadius ) in lines 10 and 46 instead of if( abs(fDist) > _S.fRadius ) .
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 |
bool SphereTriangleCollision( const Sphere& _S, const Triangle& _T ) { Vec3 A = _T.v1-_T.v0; Vec3 B = _T.v2-_T.v1; Vec3 C = _T.v2-_T.v0; // Distance sphere plane - do not collide with back faces float fDist = dot( _T.n, _S.vCenter-_T.v0 ); if( abs(fDist) > _S.fRadius ) return false; // Circle point one the plane Vec3 P = _S.vCenter - _T.n * fDist; // Closest point on all edges Vec3 P_v0 = P-_T.v0; Vec3 P_v1 = P-_T.v1; Vec3 CoE1 = _T.v0 + A * saturate( dot( P_v0, A) / lensq(A) ); Vec3 CoE2 = _T.v0 + C * saturate( dot( P_v0, C) / lensq(C) ); Vec3 CoE3 = _T.v1 + B * saturate( dot( P_v1, B) / lensq(B) ); // The vertex on the opposite side of the edge cannot lie in the same // direction as the nearest point if P lies inside the triangle. bool bInside = dot( CoE1-P, _T.v2-P ) < 0.0f; bInside &= dot( CoE2-P, P_v1 ) > 0.0f; // Inverse sign because of use from P-v1 bInside &= dot( CoE3-P, P_v0 ) > 0.0f; // Inverse sign because of use from P-v0 if( bInside ) return true; // Search for a collision on a edge or vertex if( lensq(CoE1-_S.vCenter) < _S.fRadius * _S.fRadius ) return true; if( lensq(CoE2-_S.vCenter) < _S.fRadius * _S.fRadius ) return true; return ( lensq(CoE3-_S.vCenter) < _S.fRadius * _S.fRadius ); } bool SphereTriangleCollision( const Sphere& _S, const Triangle& _T, Vec3& _vResolve ) { Vec3 A = _T.v1-_T.v0; Vec3 B = _T.v2-_T.v1; Vec3 C = _T.v2-_T.v0; // Distance sphere plane float fDist = dot( _T.n, _S.vCenter-_T.v0 ); if( abs(fDist) > _S.fRadius ) return false; // Circle point one the plane Vec3 P = _S.vCenter - _T.n * fDist; // Closest point on all edges Vec3 P_v0 = P-_T.v0; Vec3 P_v1 = P-_T.v1; Vec3 CoE1 = _T.v0 + A * saturate( dot( P_v0, A) / lensq(A) ); Vec3 CoE2 = _T.v0 + C * saturate( dot( P_v0, C) / lensq(C) ); Vec3 CoE3 = _T.v1 + B * saturate( dot( P_v1, B) / lensq(B) ); // The vertex on the opposite side of the edge cannot lie in the same // direction as the nearest point if P lies inside the triangle. bool bInside = dot( CoE1-P, _T.v2-P ) < 0.0f; bInside &= dot( CoE2-P, P_v1 ) > 0.0f; // Inverse sign because of use from P-v1 bInside &= dot( CoE3-P, P_v0 ) > 0.0f; // Inverse sign because of use from P-v0 if( bInside ) { // COLLISION inside the triangle _vResolve = _T.n * max( 0.0f, _S.fRadius - abs(fDist) ) * sgn(fDist); return true; } // Search for a collision on a edge or vertex Vec3 vShortest(CoE1-_S.vCenter); float fLenShortest = lensq(vShortest); fDist = lensq(CoE2-_S.vCenter); if( fDist < fLenShortest ) { fLenShortest = fDist; vShortest = CoE2-_S.vCenter; } fDist = lensq(CoE3-_S.vCenter); if( fDist < fLenShortest ) { fLenShortest = fDist; vShortest = CoE3-_S.vCenter; } // Collision on edge or vertex if( fLenShortest < _S.fRadius * _S.fRadius ) { fLenShortest = sqrt(fLenShortest); _vResolve = vShortest * (( fLenShortest - _S.fRadius ) / fLenShortest); return true; } return false; } |